Binary

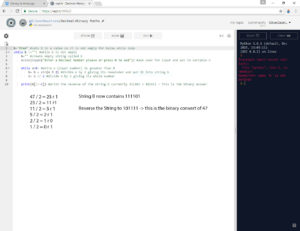
Whereas we think of number as being expressed in Base 10, Decimal or Denary using digits 0-9 it’s much easier for computers to work with just two numbers 0 and 1. These two numbers can represent a transistor or microscopic switch in the computer which turns on and off as electricity flows through it. When these series of 0 and 1 are put together they can form the basis of all data and information contained on the computer from text to image s to music and videos.

In base 10 we use something called place value so that the same digit can represent different values of numbers.

Thousands	Hundreds	Tens	Units
2	3	9	5

The table above represents the number 2395 in base 10 or 2395₁₀

In binary this same place value system can be used to represent different numbers using just the 0 and 1.

27	26	25	24	23	22	21	20
128	64	32	16	8	4	2	1

In a binary number system there are some key words that represent a binary number.

• Bit – This a single value of a binary number either a 0 or 1
• Nibble – 4 bits (half a byte)
• Byte – 8 bits

So the binary number 0101010 is equal to 42₁₀So if we take all the columns where there is a 1 we get 32+8+2 = 42

If we wanted to find what the number 27 in binary, we would look at the table, put a 1 in the largest possible number that divides into 27. In this case 32 will not but 16 will. This leaves 11, so 8 will go into 11 so we put a one in that column, leaves us 3. 4 will not go in to 3 so we put a 0, but 2 will so we put a 1. This leaves a final number of 1. Well 1 will divide into 1 so we can put a 1 in that column. As the number 27 is and odd number we will always have a 1 in the last column. If it was an even number we would have a 0.

64	32	16	8	4	2	1
0	0	1	1	0	1	1

So the answer 27₁₀ is 0011011₂

We can remove the leading 0’s as they are not required. Which leaves 11011₂

In programming you would use a more mathematical approach to conversion. A practical example can be seen in the image below. It dived the starting denary number by 2, then takes the remainder values and forms a binary number, then reverses it to get the correct result.

Computers seem incredibly smart machines, however they are in fact incredibly simple. In basic terms all a computer can do is add up binary numbers. However it does this very quickly.

To perform binary additions the process is rather simple.

The two ways to perform the calculation with binary numbers 0010 + 0111

Convert both to denary and add them together:

Place	8	4	2	1	Denary
Number 1	0	0	1	0	2
Number 2	0	1	1	1	7
					9

The denary numbers are 2+7=9

The other method is to perform addition on the binary numbers themselves, using the following rules:

0+0 = 0

0+1 = 1

1+0 = 1

1+1 = 0 carry 1

Place	8	4	2	1
Number 1	0	0	1	0
Number 2	0	1	1	1
Sum	1	0	0	1
Carry	1	1

So we have 1001 which is a 8+1=9

The below links to a Worksheet completed during the SKE on Binary.

Binary Worksheet